摘要

关键词
- 物理神经网络 (Physical neural networks, PNNs)
- 反向传播 (Backpropagation)
- 物理感知训练 (Physics-aware training, PAT)
- 深度学习加速器 (Deep learning accelerators)
- 光学非线性 (Nonlinear optics)
- 图像分类 (Image classification)
研究背景
随着深度学习模型在科学与工程领域的广泛应用,其快速增长的计算需求已经超越摩尔定律的提升,能源效率成为主要瓶颈。传统深度学习加速器主要依赖于硬件物理过程和数学运算的直接同构,但这种方法通常局限于推理阶段,难以直接应用反向传播算法训练硬件。为了突破这一局限,本文提出了一种新型物理神经网络(PNNs)方法,通过可控物理系统实现深度学习计算,并引入混合的物理感知训练策略,将物理系统训练与数字模拟相结合。这一框架为机器学习能效和速度的提升提供了全新思路,同时开辟了物理系统功能化设计的广阔前景。
创新点
- 提出混合物理感知训练算法(PAT),实现对物理神经网络的反向传播训练。
- 将光学、机械和电子系统用于物理神经网络,展示其通用性和多样性。
- 在图像和音频分类中实现高精度的物理计算,显著提高能效和计算速度。
- 将PNNs与传统数字硬件集成,构建混合物理–数字架构,实现资源的高效分配。
研究内容
本研究提出并验证了一种新型的物理感知训练(PAT)算法,能够在物理神经网络中直接应用反向传播训练。PNNs由物理层组成,每一层执行可控的物理变换,而无需与传统深度学习层的数学操作同构。实验部分涵盖三种物理系统:多模机械振荡、非线性电子振荡以及超快光学二次谐波生成(SHG),分别用于图像和音频分类任务。通过PAT,这些系统被成功训练以执行深度学习计算,在测试集上的分类精度分别达到87%、93%和97%。进一步展示了PNNs如何通过混合物理–数字架构与传统数字硬件协作,以最大限度提高能效。该研究还探讨了PNNs在智能传感器、机器人和材料设计等领域的潜在应用。
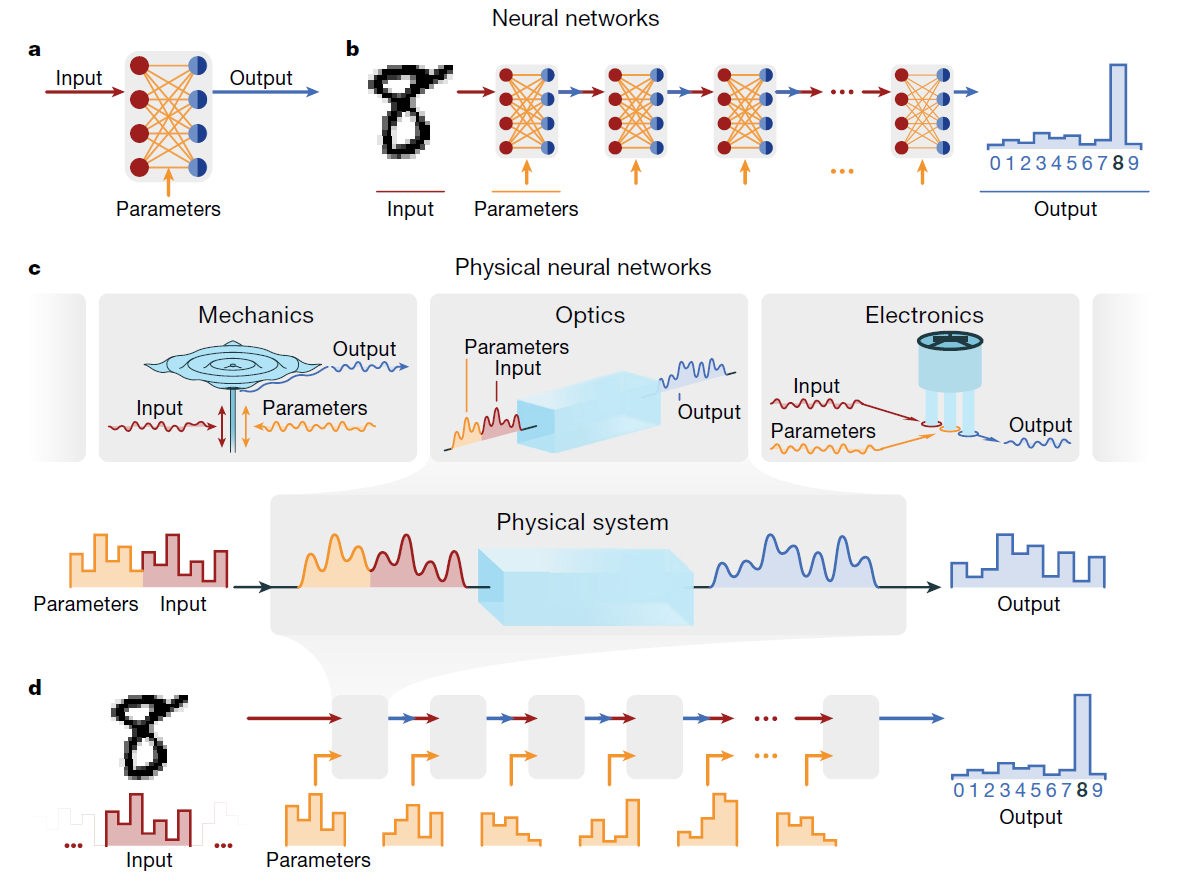
(a) 人工神经网络的基本组成单元(层):通常是可训练的矩阵-向量乘法,随后是逐元素的非线性激活函数。
(b) 深度神经网络(DNN)通过层的序列可实现输入数据的多步(分层)变换,并可训练这些变换。
(c) 物理系统在演化过程中实际上会执行某些计算。我们将其可控属性划分为输入数据和控制参数。改变参数会改变数据的变换方式。图中展示了三个示例:在机械(电子)系统中,输入数据和参数被编码为施加在金属板(非线性电路)上的时间依赖力(电压)。然后通过麦克风(示波器)测量多模振动(瞬态电压)。在非线性光学系统中,脉冲通过二阶非线性晶体,产生非线性混合输出。输入数据和参数被编码在输入脉冲的频谱中,输出从倍频脉冲的频谱中获取。
(d) 类似于由可训练的非线性数学函数序列构建的DNN,我们通过可训练的物理变换序列构建深度PNNs。在PNNs中,每个物理层实现一个可控的物理功能,而不需要与传统DNN层数学上同构。
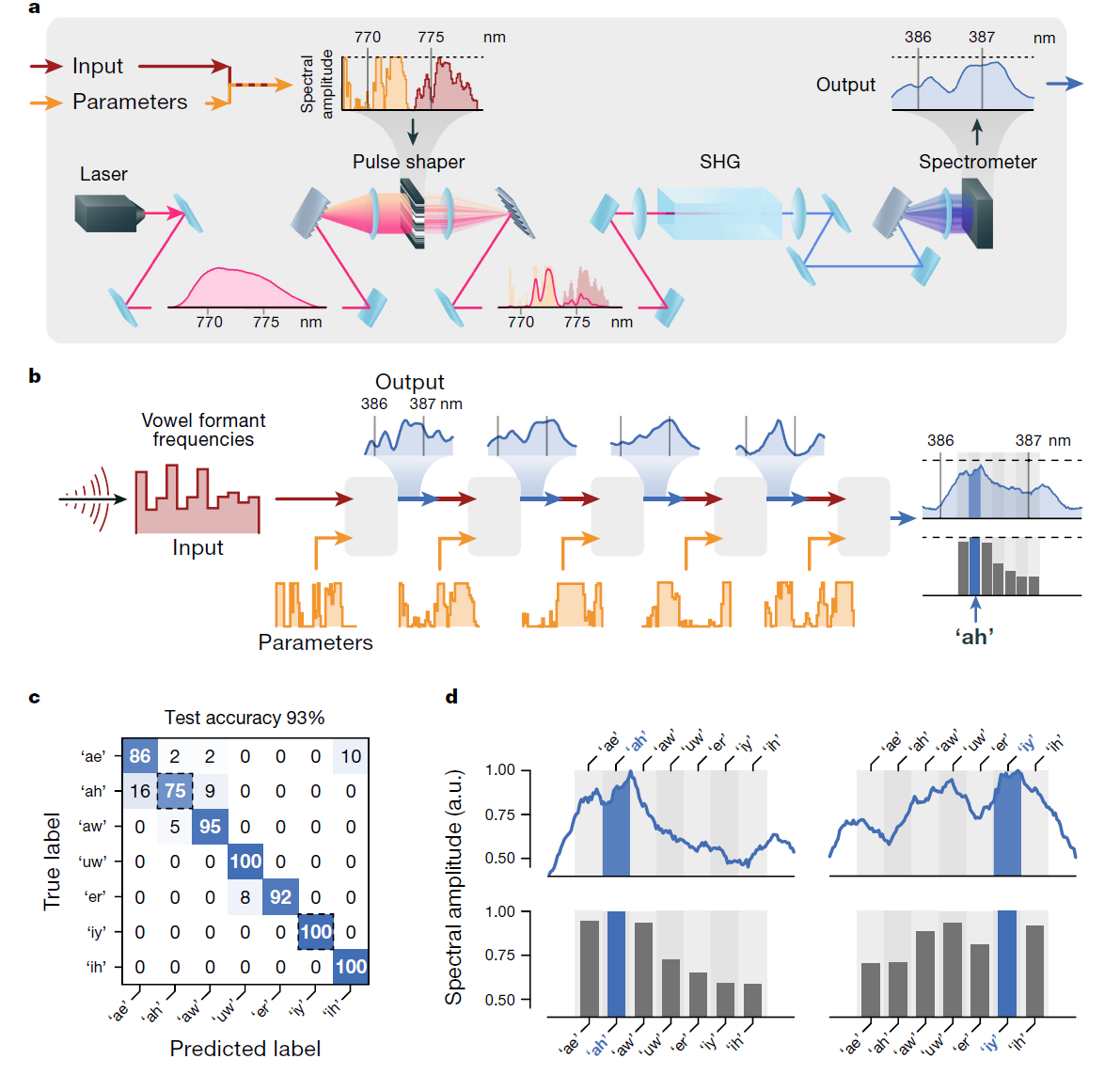
(a) 输入数据被编码到激光脉冲的频谱中(见方法和补充部分2)。为控制宽带SHG过程实现的变换,脉冲频谱的一部分被用作可训练参数(橙色)。物理计算的结果通过在二阶非线性介质中产生的约390 nm蓝光脉冲的频谱获取。
(b) 为构建深度PNN,SHG变换的输出被用作后续SHG变换的输入,每层有独立的可训练参数。
(c, d) 训练SHG-PNN(见正文和图3)后,其在测试元音分类任务上的准确率为93%。
(c) PNN在测试集上的混淆矩阵。
(d) 代表性的最终层输出频谱示例,展示了SHG-PNN的预测结果。
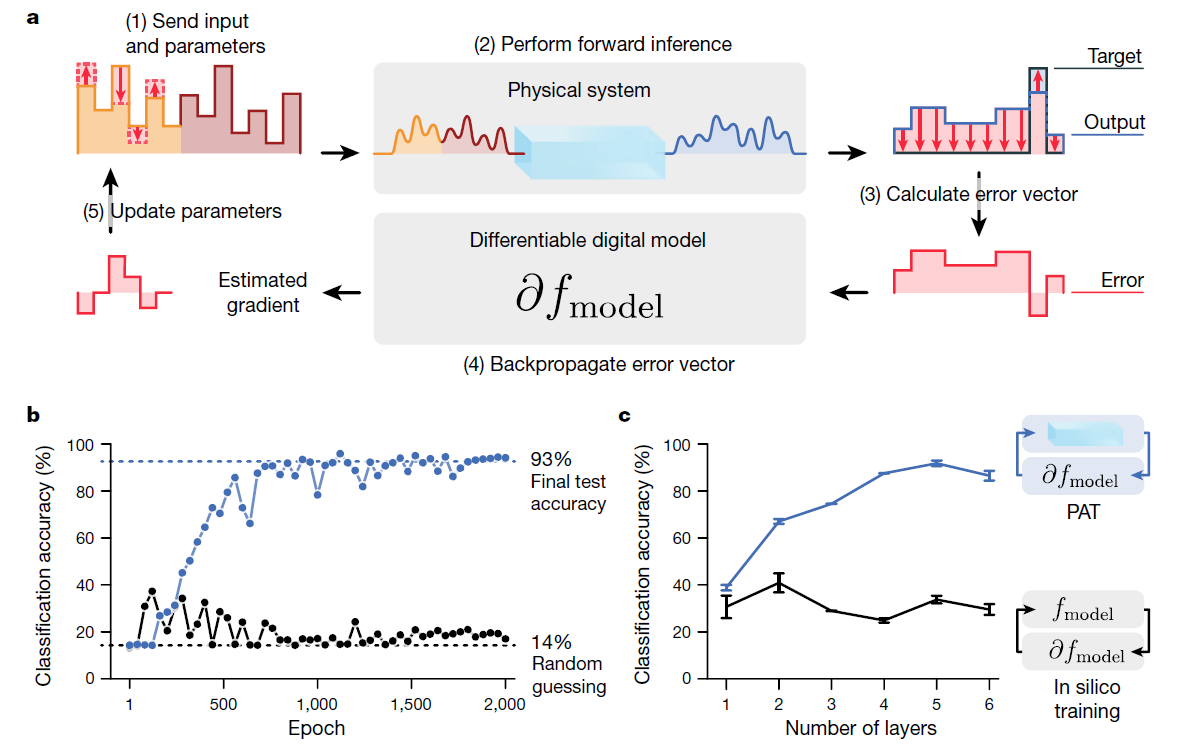
(a) PAT是一种混合物理–数字算法,用于通过反向传播训练可控物理参数,使物理系统能够准确地执行机器学习任务,即使在建模误差和物理噪声的存在下。与完全依赖数字模型的训练不同(即纯数字训练),PAT使用物理系统执行前向计算。虽然图中仅显示了一层,PAT自然地扩展到多层架构(见方法)。
(b) 对比实验中SHG-PNN(图2b)的验证准确率与训练轮次,分别采用PAT和纯数字训练。
(c) 使用PAT和纯数字训练方法,具有不同物理层数量的SHG-PNN的最终实验测试准确率。误差棒的长度表示两倍标准误差。
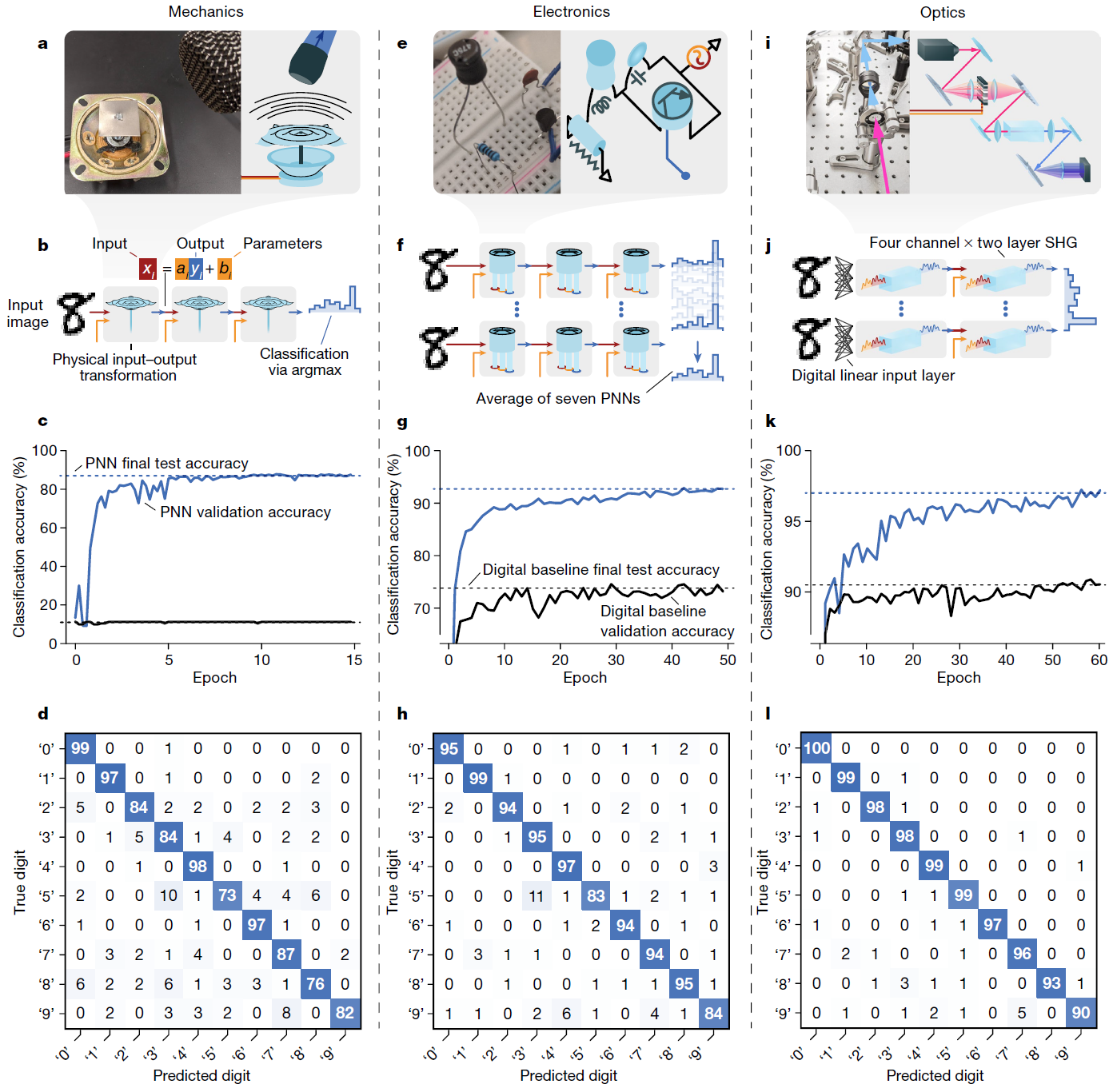
我们基于三种物理系统(机械、电子和光学)训练PNNs来分类手写数字图像。
(a) 机械PNN:金属板的多模振动由编码输入图像数据和参数的时间依赖力驱动。
(b) 机械PNN的多层架构。
(c) 使用PAT训练的机械PNN验证分类准确率与训练轮次的关系曲线,同时展示了参考模型的曲线,其中由扬声器实现的物理变换被替换为恒等操作。
(d) 机械PNN训练后的混淆矩阵。
(e-h) 对非线性模拟电子PNN的(a-d)部分分别进行类似描述。
(i-l) 对基于宽带光学SHG的混合物理–数字PNN的(a-d)部分分别进行类似描述。机械、电子和光学PNN的最终测试准确率分别为87%、93%和97%。
结论与展望
本文提出的物理神经网络(PNNs)及其训练框架物理感知训练(PAT),为能效优化和功能化设计提供了新视角。PNNs不仅适用于深度学习加速器,还能用于处理物理域中的数据,尤其适用于低功耗智能传感器等场景。未来研究可进一步优化PAT算法,并探索更广泛的物理系统应用,例如非电子硬件、机器人和材料设计等领域,从而推动PNNs的实际应用和产业化进程。
论文直达
原文标题:Deep physical neural networks trained with backpropagation
Nature 2022, 601, 549–555.
点击以下链接阅读原文:

