Nature：自旋轨道耦合邻近效应增强的双层石墨烯超导性

摘要

摘要图
本研究通过将单层二硒化钨 (WSe₂) 与伯纳尔堆叠双层石墨烯 (BLG) 相结合，显著增强了其超导性。实验发现，自旋轨道耦合 (SOC) 的引入使得超导态在零磁场下出现，并在载流子密度和电场范围内展现出大幅扩展。临界温度 \(T_c\) 增加了一个数量级，达到约 300 mK。此外，平面内磁场下的测量显示，超导临界场表现出非凡的掺杂依赖性，揭示了超导态与谷极化态及 SOC 的复杂相互作用。该研究为石墨烯基超导器件的调控提供了新的思路。

关键词

  • 双层石墨烯 (Bilayer graphene)
  • 自旋轨道耦合 (Spin–orbit coupling)
  • 超导性增强 (Enhanced superconductivity)
  • 电场调控 (Electric field tuning)
  • 谷极化 (Valley polarization)
  • 伊辛超导性 (Ising superconductivity)

研究背景

双层石墨烯以其丰富的对称性破缺相闻名，例如谷极化态和磁场诱导的超导性。然而，传统的双层石墨烯超导性较弱，临界温度低，仅在极窄的载流子密度范围内出现。近年来，自旋轨道耦合的引入为调控石墨烯电子特性提供了新的可能性。通过将双层石墨烯与二硒化钨结合，本研究展示了如何利用 SOC 显著增强超导性。SOC 通过改变电子波函数分布和增强电子间的相互作用，为探索高性能石墨烯超导器件提供了重要启示。

创新点

  • 首次在双层石墨烯中引入 WSe₂，通过自旋轨道邻近效应增强超导性。
  • 超导性从磁场依赖性转变为零磁场下稳定存在。
  • 超导临界温度增加了一个数量级，载流子密度范围扩大至原来的八倍。
  • 揭示了 SOC 在选择有利于库珀对形成的对称性破缺顺序中的关键作用。

研究内容

本研究通过构建 WSe₂-BLG 异质结构，引入伊辛型自旋轨道耦合，从而显著增强了双层石墨烯的超导性。实验发现，在施加垂直电场的条件下，电子波函数向 WSe₂ 层极化，诱导了显著的 SOC。测量表明，超导性出现在电场和载流子密度的广泛范围内，临界温度达到约 300 mK，并且表现出强烈的电场不对称性。在平面内磁场下，超导临界场表现出掺杂依赖性，低掺杂区域的帕里极限被显著违反。此外，通过量子振荡分析，研究发现超导相与谷极化态密切相关，SOC 是超导增强的关键因素。本研究通过结合实验和理论，为调控石墨烯中超导相提供了新的途径。

图1
图 1 | BLG-WSe2 的相图与零磁场超导现象。

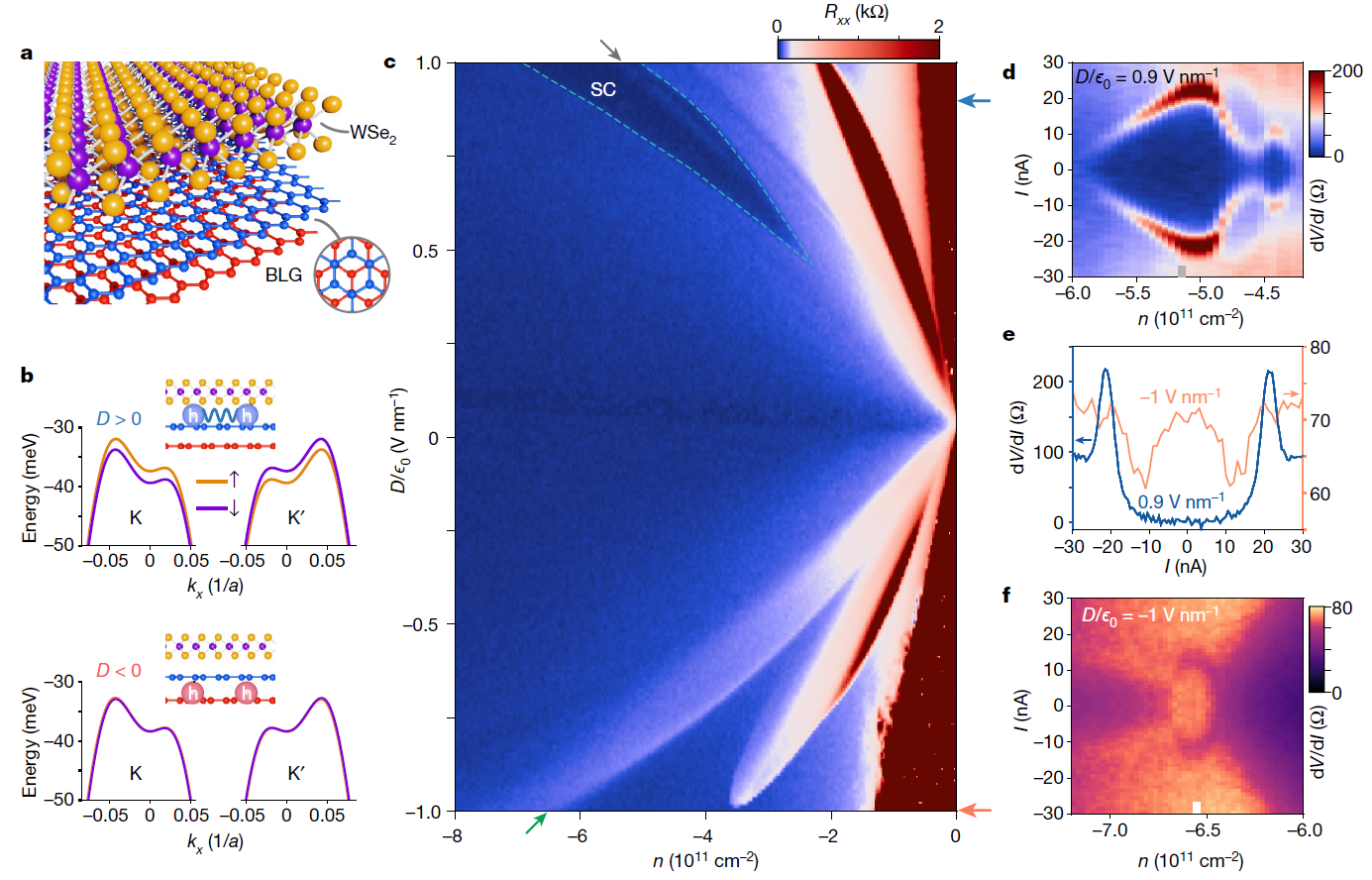
(a) BLG-WSe2 结构示意图，展示了 BLG（蓝色和红色）和 WSe2 单层（黄色和紫色）的晶格结构。
(b) 在 K 和 K′ 点附近的布里渊区中，D/ϵ0 = +1 V nm⁻¹（顶部）和 −1 V nm⁻¹（底部）下的非相互作用价带，计算中包含了顶部层的 Ising 自旋轨道耦合（SOC, λI = 1 meV）。
(c) 在零磁场下测得的纵向电阻 \(R_{xx}\) 随掺杂密度 \(n\) 和位移场 \(D\) 的变化。标志性特征为超导区域（虚线框），其分布在正位移场 \(D > 0\) 下的宽广掺杂与 \(D\) 范围中。
(d) 在 D/ϵ0 = 0.9 V nm⁻¹ 和不同 \(n\) 值下，\(dV/dI\) 与偏置电流 \(I\) 的关系图。
(e) 蓝色和橙色曲线为 (d) 和 (f) 中标记的灰色和白色条区域下的 \(n\) 线性切片数据。
(f) 在 D/ϵ0 = −1 V nm⁻¹ 时，与 (d) 类似的测量。

图2
图 2 | 超导相随温度和外磁场的演化。

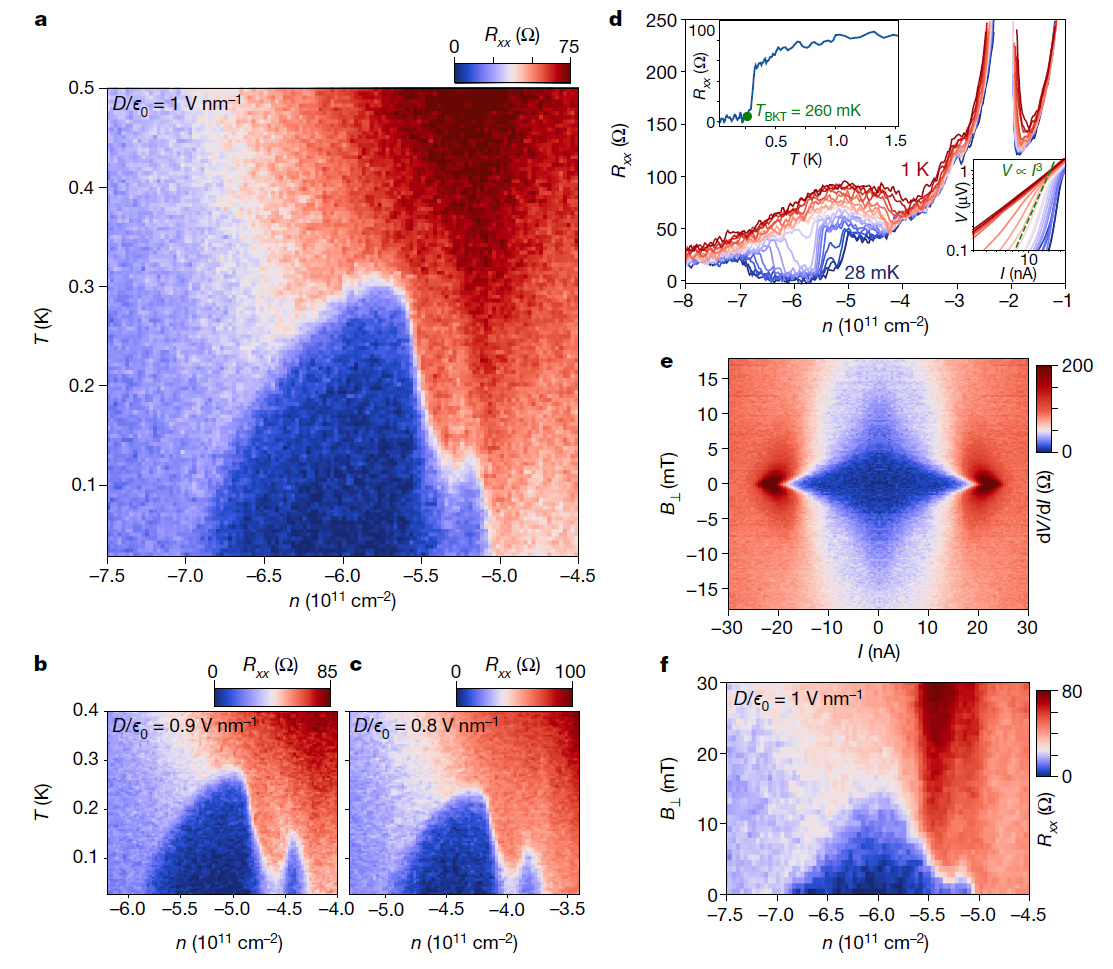
(a-c) 在不同正 D/ϵ0 值下 (\(1\), \(0.9\), \(0.8\) V nm⁻¹)，纵向电阻 \(R_{xx}\) 随掺杂密度 \(n\) 和温度的变化，展示出 FP(2,2)+ 相内的超导穹顶。灰色箭头标示了与竞争的电阻相交区域。
(d) 在 D/ϵ0 = 1 V nm⁻¹ 时的温度范围（从 28 mK 至 1 K）下 \(R_{xx}\) 随 \(n\) 的线性切片；顶部插图为在 \(n = −5.75 × 10^{11}\) cm⁻² 处测量的超导转变温度，底部插图为相应的 \(V–I\) 曲线，绿色虚线表示 \(V ∝ I^3\) 的位置，用以估算 Berezinskii-Kosterlitz-Thouless (BKT) 转变温度 \(T_\text{BKT} ≈ 260\) mK。
(e) 在 \(D/ϵ0 = 0.9\) V nm⁻¹ 和 \(n = −5.05 × 10^{11}\) cm⁻² 处测量的临界电流随外磁场 \(B_\perp\) 的变化。
(f) 在 D/ϵ0 = 1 V nm⁻¹ 时，\(R_{xx}\) 随 \(n\) 和外磁场 \(B_\perp\) 的变化图，标注了超导区域。

图3
图 3 | 超导态的费米面结构。

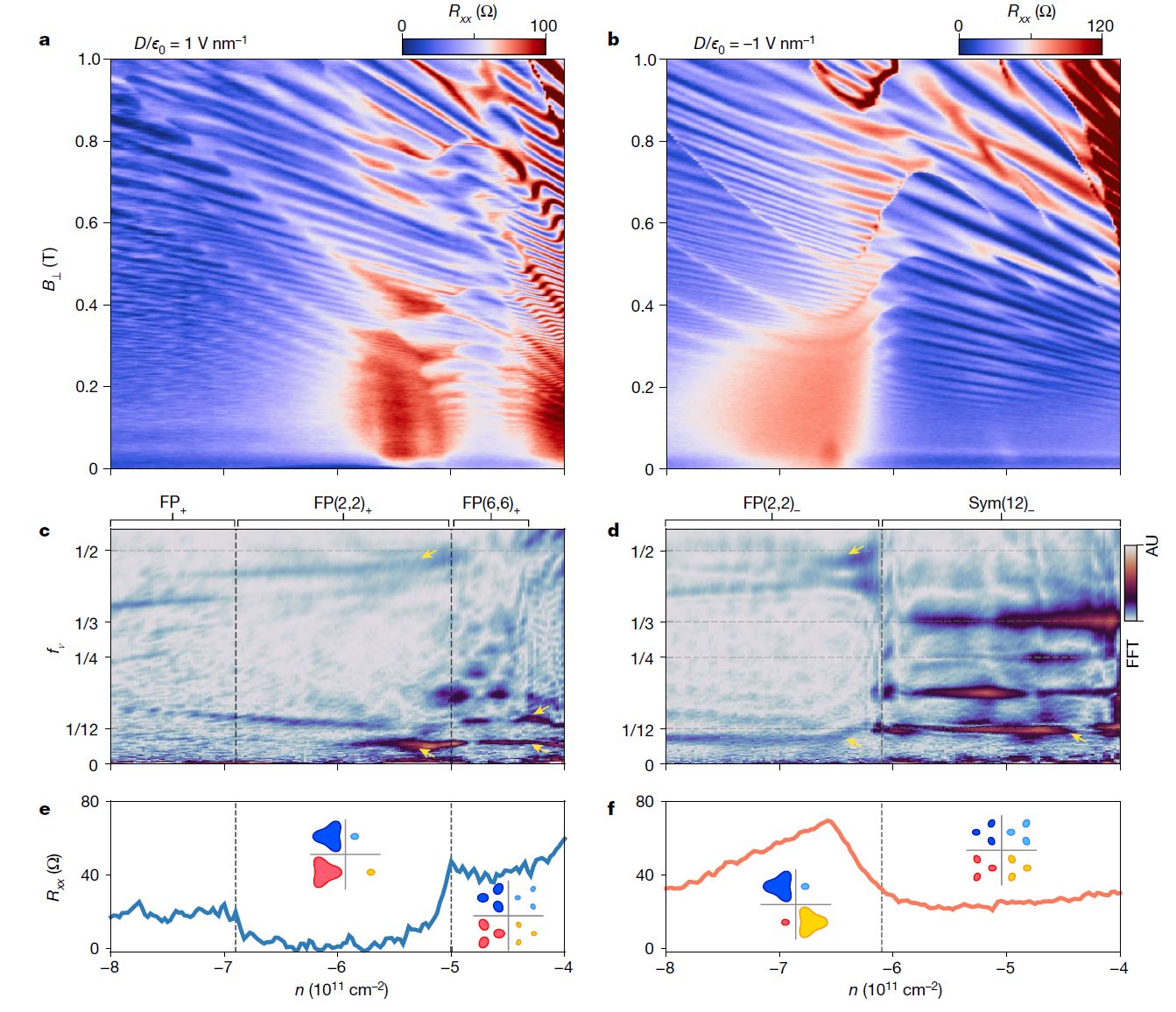
(a-b) 在 D/ϵ0 = 1 V nm⁻¹ 和 −1 V nm⁻¹ 时，纵向电阻 \(R_{xx}\) 随外磁场 \(B_\perp\) 和掺杂密度 \(n\) 的变化。
(c-d) \(R_{xx}(1/B_\perp)\) 的快速傅里叶变换 (FFT)，\(f_ν\) 表示旋周期包围的总费米面面积分数，标注了相应 FFT 峰值。FFT 分别来自 (a) 和 (b) 中的 \(0.05 T < B_\perp < 0.6 T\) 数据。
(e-f) \(R_{xx}\) 随 \(n\) 的切片图，分别对应 D/ϵ0 = 1 V nm⁻¹ 的超导区域和 −1 V nm⁻¹ 的电阻区域。

图4
图 4 | 掺杂依赖的 Pauli 限制违背。

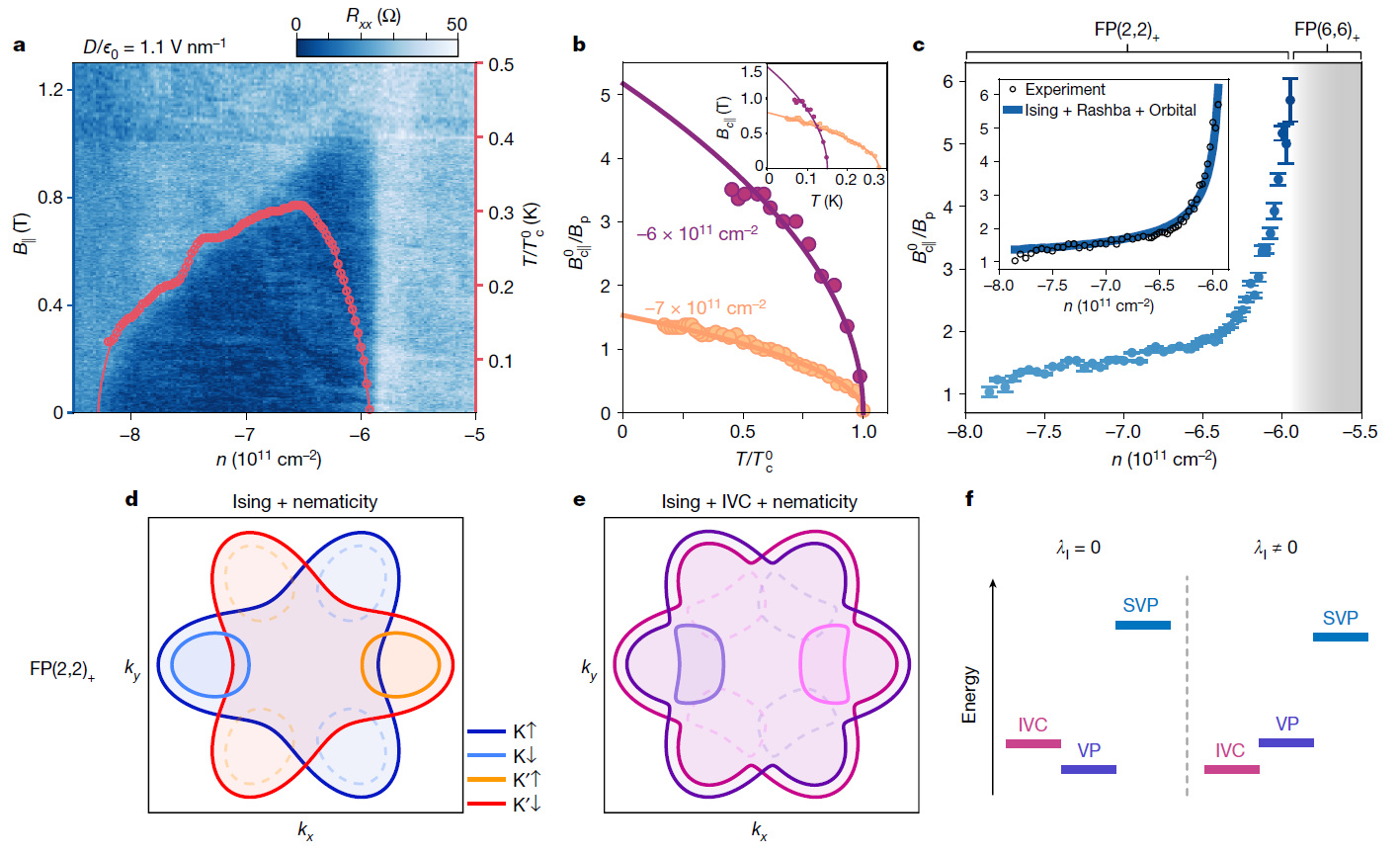
(a) 在 D/ϵ0 = 1.1 V nm⁻¹ 时，纵向电阻 \(R_{xx}\) 随平面内磁场 \(B_\parallel\) 和掺杂密度 \(n\) 的变化。红色曲线描绘了超导穹顶，开放圆点标示了零磁场时的临界温度 \(T_c^0\)。
(b) 临界磁场 \(B_c^\parallel\) 与 Pauli 限制场 \(B_p = 1.86 T_c^0\) 的比值随归一化温度 \(T/T_c^0\) 的变化。在两种代表性掺杂下，数据符合经验公式 \(T/T_c^0 = 1 - (B_c^\parallel/B_p)^2\)。
(c) \(B_c^\parallel/B_p\) 随掺杂密度 \(n\) 的变化。误差条表示拟合中获得的标准差。插图显示了包含 Ising SOC 和掺杂相关 Rashba SOC 的模型预测曲线。
(d-e) FP(2,2)+ 相的费米面结构示意图，分别带有 Ising SOC 和相间电荷序 (IVC) 的次序。虚线对应无序的情况。
(f) 提议的场景示意图，其中 Ising SOC 倾向于促进有利于超导配对的 IVC 次序。

结论与展望

本研究表明，通过引入 WSe₂ 的邻近效应和自旋轨道耦合，可以显著增强双层石墨烯的超导性，拓展其工作范围和性能。未来的研究可进一步优化异质结构设计，探索其他过渡金属二硫化物与石墨烯的结合，以开发高性能、可调控的二维超导器件。

论文直达

原文标题：Enhanced superconductivity in spin–orbit proximitized bilayer graphene

Nature 2023, 613, 268–273.

点击以下链接阅读原文：

原论文链接 >>>